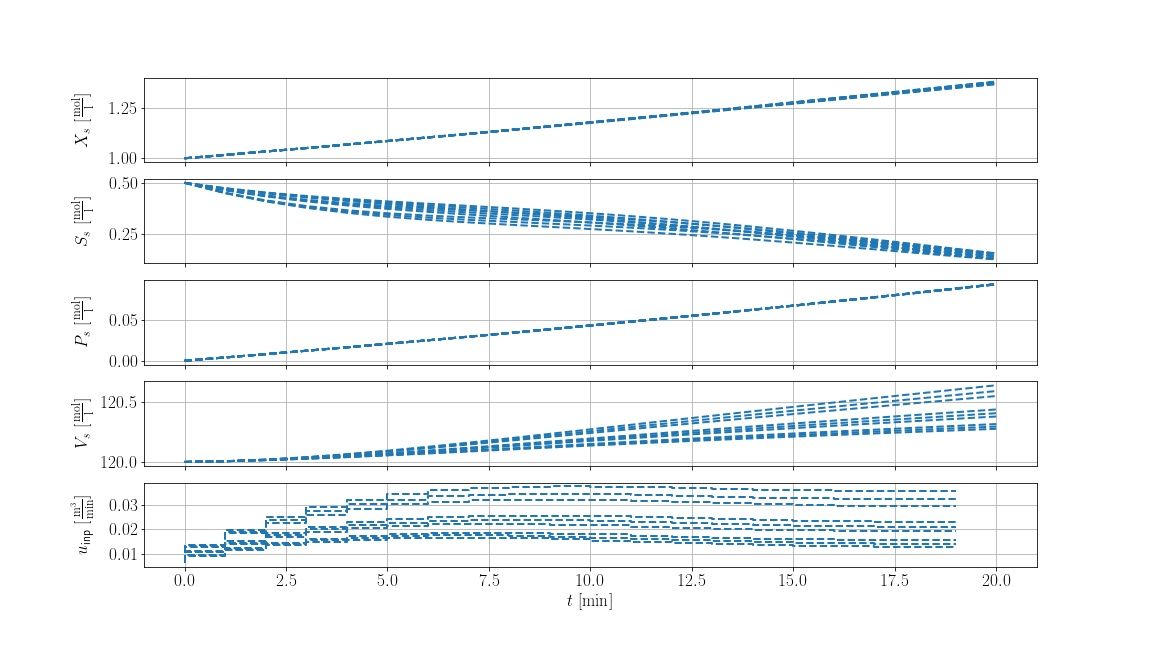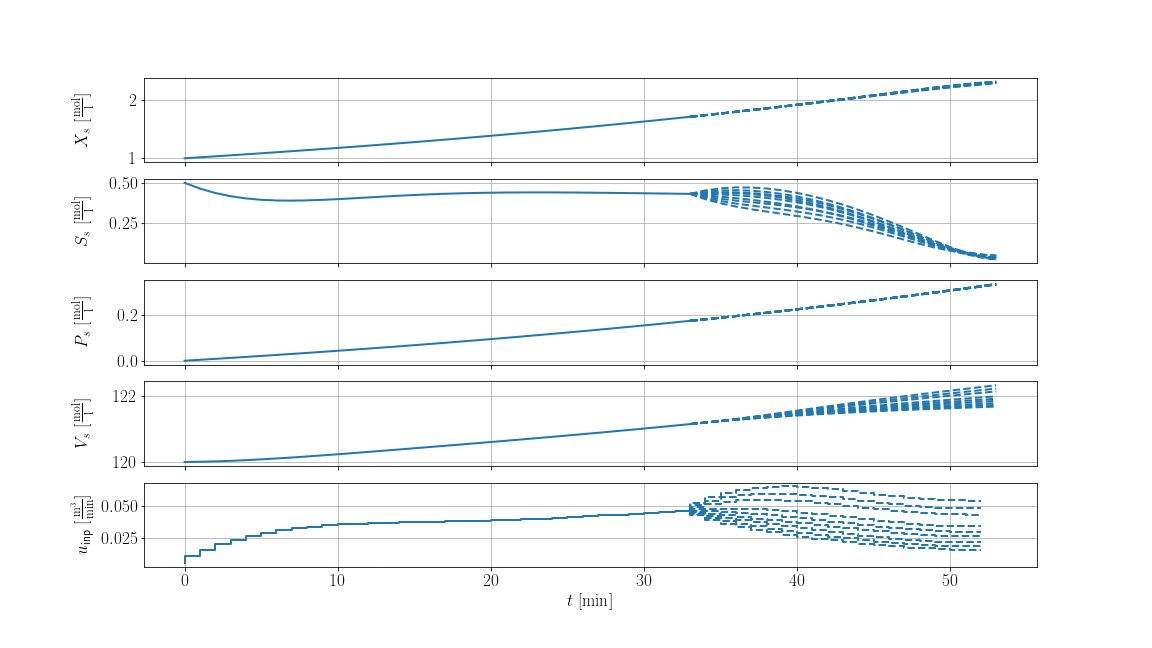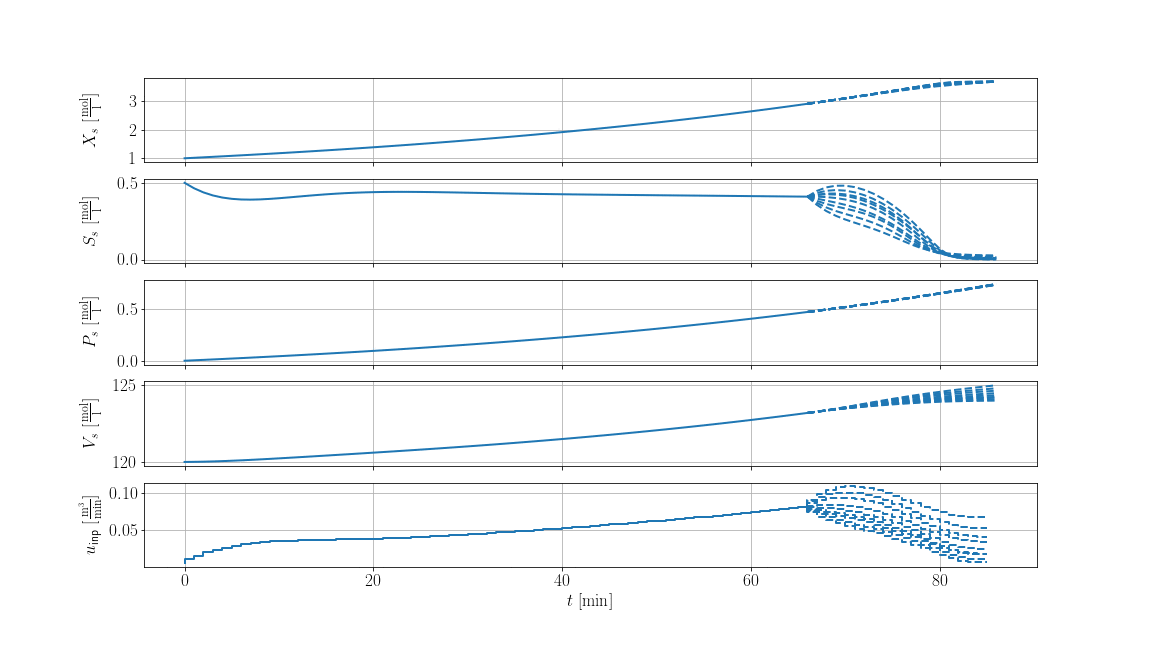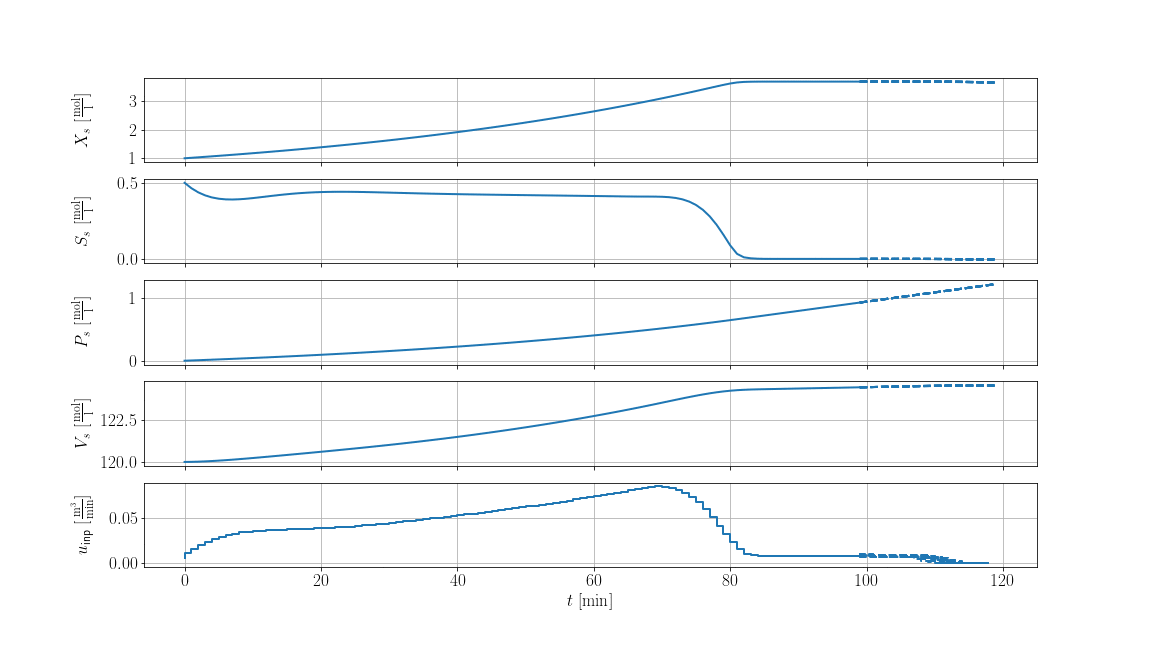Batch Bioreactor#
In this Jupyter Notebook we illustrate the example batch_reactor.
Open an interactive online Jupyter Notebook with this content on Binder:
The example consists of the three modules template_model.py, which describes the system model, template_mpc.py, which defines the settings for the control and template_simulator.py, which sets the parameters for the simulator. The modules are used in main.py for the closed-loop execution of the controller.
In the following the different parts are presented. But first, we start by importing basic modules and do-mpc.
[1]:
import numpy as np
import sys
from casadi import *
# Add do_mpc to path. This is not necessary if it was installed via pip
import os
rel_do_mpc_path = os.path.join('..','..','..')
sys.path.append(rel_do_mpc_path)
# Import do_mpc package:
import do_mpc
Model#
In the following we will present the configuration, setup and connection between these blocks, starting with the model.
The considered model of the batch bioreactor is continuous and has 4 states and 1 control input, which are depicted below:
The model is initiated by:
[2]:
model_type = 'continuous' # either 'discrete' or 'continuous'
model = do_mpc.model.Model(model_type)
States and control inputs#
The four states are concentration of the biomass \(X_{\text{s}}\), the concentration of the substrate \(S_{\text{s}}\), the concentration of the product \(P_{\text{s}}\) and the volume \(V_{\text{s}}\):
[3]:
# States struct (optimization variables):
X_s = model.set_variable('_x', 'X_s')
S_s = model.set_variable('_x', 'S_s')
P_s = model.set_variable('_x', 'P_s')
V_s = model.set_variable('_x', 'V_s')
The control input is the feed flow rate \(u_{\text{inp}}\) of \(S_{\text{s}}\):
[4]:
# Input struct (optimization variables):
inp = model.set_variable('_u', 'inp')
ODE and parameters#
The system model is described by the ordinary differential equation:
\begin{align} \dot{X}_{\text{s}} &=\mu(S_{\text{s}})X_{\text{s}}-\frac{u_{\text{inp}}}{V_{\text{s}}}X_{\text{s}},\\ \dot{S}_{\text{s}} &=-\frac{\mu(S_{\text{s}})X_{\text{s}}}{Y_{\text{x}}}-\frac{vX_{\text{s}}}{Y_{\text{p}}}+\frac{u_{\text{inp}}}{V_{\text{s}}}(S_{\text{in}}-S_{\text{s}}),\\ \dot{P}_{\text{s}} &=vX_{\text{s}}-\frac{u_{\text{inp}}}{V_{\text{s}}}P_{\text{s}},\\ \dot{V}_{\text{s}} &=u_{\text{inp}},\\ \end{align}
where:
\begin{align} \mu(S_{\text{s}})&=\frac{\mu_{\text{m}} S_{\text{s}}}{K_{\text{m}}+S_{\text{s}}+(S_{\text{s}}^2/K_{\text{i}})}, \end{align}
\(S_{\text{in}}\) is the inlet substrate concentration, \(\mu_{\text{m}}\), \(K_{\text{m}}\), \(K_{\text{i}}\) and \(v\) are kinetic parameters \(Y_{\text{x}}\) and \(Y_{\text{p}}\) are yield coefficients. The inlet substrate concentration \(S_{\text{in}}\) and the \(Y_{\text{x}}\) are uncertain while the rest of the parameters is considered certain:
[5]:
# Certain parameters
mu_m = 0.02
K_m = 0.05
K_i = 5.0
v_par = 0.004
Y_p = 1.2
# Uncertain parameters:
Y_x = model.set_variable('_p', 'Y_x')
S_in = model.set_variable('_p', 'S_in')
In the next step, the ODE for each state is set:
[6]:
# Auxiliary term
mu_S = mu_m*S_s/(K_m+S_s+(S_s**2/K_i))
# Differential equations
model.set_rhs('X_s', mu_S*X_s - inp/V_s*X_s)
model.set_rhs('S_s', -mu_S*X_s/Y_x - v_par*X_s/Y_p + inp/V_s*(S_in-S_s))
model.set_rhs('P_s', v_par*X_s - inp/V_s*P_s)
model.set_rhs('V_s', inp)
Finally, the model setup is completed:
[7]:
# Build the model
model.setup()
Controller#
Next, the controller is configured. First, one member of the mpc class is generated with the prediction model defined above:
[8]:
mpc = do_mpc.controller.MPC(model)
We choose the prediction horizon n_horizon, set the robust horizon n_robust to 3. The time step t_step is set to one second and parameters of the applied discretization scheme orthogonal collocation are as seen below:
[9]:
setup_mpc = {
'n_horizon': 20,
'n_robust': 1,
'open_loop': 0,
't_step': 1.0,
'state_discretization': 'collocation',
'collocation_type': 'radau',
'collocation_deg': 2,
'collocation_ni': 2,
'store_full_solution': True,
# Use MA27 linear solver in ipopt for faster calculations:
#'nlpsol_opts': {'ipopt.linear_solver': 'MA27'}
}
mpc.set_param(**setup_mpc)
Objective#
The batch bioreactor is used to produce penicillin. Hence, the objective of the controller is to maximize the concentration of the product \(P_{\text{s}}\). Additionally, we add a penalty on input changes, to obtain a smooth control performance.
[10]:
mterm = -model.x['P_s'] # terminal cost
lterm = -model.x['P_s'] # stage cost
mpc.set_objective(mterm=mterm, lterm=lterm)
mpc.set_rterm(inp=1.0) # penalty on input changes
Constraints#
In the next step, the constraints of the control problem are set. In this case, there are only upper and lower bounds for each state and the input:
[11]:
# lower bounds of the states
mpc.bounds['lower', '_x', 'X_s'] = 0.0
mpc.bounds['lower', '_x', 'S_s'] = -0.01
mpc.bounds['lower', '_x', 'P_s'] = 0.0
mpc.bounds['lower', '_x', 'V_s'] = 0.0
# upper bounds of the states
mpc.bounds['upper', '_x','X_s'] = 3.7
mpc.bounds['upper', '_x','P_s'] = 3.0
# upper and lower bounds of the control input
mpc.bounds['lower','_u','inp'] = 0.0
mpc.bounds['upper','_u','inp'] = 0.2
Uncertain values#
The explicit values of the two uncertain parameters \(Y_{\text{x}}\) and \(S_{\text{in}}\), which are considered in the scenario tree, are given by:
[12]:
Y_x_values = np.array([0.5, 0.4, 0.3])
S_in_values = np.array([200.0, 220.0, 180.0])
mpc.set_uncertainty_values(Y_x = Y_x_values, S_in = S_in_values)
This means with n_robust=1, that 9 different scenarios are considered. The setup of the MPC controller is concluded by:
[13]:
mpc.setup()
Estimator#
We assume, that all states can be directly measured (state-feedback):
[14]:
estimator = do_mpc.estimator.StateFeedback(model)
Simulator#
To create a simulator in order to run the MPC in a closed-loop, we create an instance of the do-mpc simulator which is based on the same model:
[15]:
simulator = do_mpc.simulator.Simulator(model)
For the simulation, we use the time step t_step as for the optimizer:
[16]:
params_simulator = {
'integration_tool': 'cvodes',
'abstol': 1e-10,
'reltol': 1e-10,
't_step': 1.0
}
simulator.set_param(**params_simulator)
Realizations of uncertain parameters#
For the simulatiom, it is necessary to define the numerical realizations of the uncertain parameters in p_num. First, we get the structure of the uncertain parameters:
[17]:
p_num = simulator.get_p_template()
We define a function which is called in each simulation step, which gives the current realization of the uncertain parameters, with respect to defined inputs (in this case t_now):
[18]:
p_num['Y_x'] = 0.4
p_num['S_in'] = 200.0
# function definition
def p_fun(t_now):
return p_num
# Set the user-defined function above as the function for the realization of the uncertain parameters
simulator.set_p_fun(p_fun)
By defining p_fun as above, the function will always return the same values. To finish the configuration of the simulator, call:
[19]:
simulator.setup()
Closed-loop simulation#
For the simulation of the MPC configured for the batch bioreactor, we inspect the file main.py. We define the initial state of the system and set for all parts of the closed-loop configuration:
[20]:
# Initial state
X_s_0 = 1.0 # Concentration biomass [mol/l]
S_s_0 = 0.5 # Concentration substrate [mol/l]
P_s_0 = 0.0 # Concentration product [mol/l]
V_s_0 = 120.0 # Volume inside tank [m^3]
x0 = np.array([X_s_0, S_s_0, P_s_0, V_s_0])
# Set for controller, simulator and estimator
mpc.x0 = x0
simulator.x0 = x0
estimator.x0 = x0
mpc.set_initial_guess()
Prepare visualization#
For the visualization of the control performance, we first import matplotlib and change some basic settings:
[21]:
import matplotlib.pyplot as plt
plt.ion()
from matplotlib import rcParams
rcParams['text.usetex'] = True
rcParams['text.latex.preamble'] = [r'\usepackage{amsmath}',r'\usepackage{siunitx}']
rcParams['axes.grid'] = True
rcParams['lines.linewidth'] = 2.0
rcParams['axes.labelsize'] = 'xx-large'
rcParams['xtick.labelsize'] = 'xx-large'
rcParams['ytick.labelsize'] = 'xx-large'
We use the plotting capabilities, which are included in do-mpc. The mpc_graphics contain information like the current estimated state and the predicted trajectory of the states and inputs based on the solution of the control problem. The sim_graphics contain the information about the simulated evaluation of the system.
[22]:
mpc_graphics = do_mpc.graphics.Graphics(mpc.data)
sim_graphics = do_mpc.graphics.Graphics(simulator.data)
A figure containing the 4 states and the control input are created:
[23]:
%%capture
fig, ax = plt.subplots(5, sharex=True, figsize=(16,9))
fig.align_ylabels()
for g in [sim_graphics,mpc_graphics]:
# Plot the state on axis 1 to 4:
g.add_line(var_type='_x', var_name='X_s', axis=ax[0], color='#1f77b4')
g.add_line(var_type='_x', var_name='S_s', axis=ax[1], color='#1f77b4')
g.add_line(var_type='_x', var_name='P_s', axis=ax[2], color='#1f77b4')
g.add_line(var_type='_x', var_name='V_s', axis=ax[3], color='#1f77b4')
# Plot the control input on axis 5:
g.add_line(var_type='_u', var_name='inp', axis=ax[4], color='#1f77b4')
ax[0].set_ylabel(r'$X_s~[\si[per-mode=fraction]{\mole\per\litre}]$')
ax[1].set_ylabel(r'$S_s~[\si[per-mode=fraction]{\mole\per\litre}]$')
ax[2].set_ylabel(r'$P_s~[\si[per-mode=fraction]{\mole\per\litre}]$')
ax[3].set_ylabel(r'$V_s~[\si[per-mode=fraction]{\mole\per\litre}]$')
ax[4].set_ylabel(r'$u_{\text{inp}}~[\si[per-mode=fraction]{\cubic\metre\per\minute}]$')
ax[4].set_xlabel(r'$t~[\si[per-mode=fraction]{\minute}]$')
Run closed-loop#
The closed-loop system is now simulated for 50 steps (and the ouput of the optimizer is suppressed):
[24]:
%%capture
n_steps = 100
for k in range(n_steps):
u0 = mpc.make_step(x0)
y_next = simulator.make_step(u0)
x0 = estimator.make_step(y_next)
Results#
The next cell converts the results of the closed-loop MPC simulation into a gif (might take a few minutes):
[25]:
from matplotlib.animation import FuncAnimation, FFMpegWriter, ImageMagickWriter
# The function describing the gif:
def update(t_ind):
sim_graphics.plot_results(t_ind)
mpc_graphics.plot_predictions(t_ind)
mpc_graphics.reset_axes()
if False:
anim = FuncAnimation(fig, update, frames=n_steps, repeat=False)
gif_writer = ImageMagickWriter(fps=10)
anim.save('anim_batch_reactor_final.gif', writer=gif_writer)
The result is shown below, where solid lines are the recorded trajectories and dashed lines are the predictions of the scenarios: