Model predictive control python toolbox#
do-mpc is a comprehensive open-source toolbox for robust model predictive control (MPC) and moving horizon estimation (MHE). do-mpc enables the efficient formulation and solution of control and estimation problems for nonlinear systems, including tools to deal with uncertainty and time discretization. The modular structure of do-mpc contains simulation, estimation and control components that can be easily extended and combined to fit many different applications.
In summary, do-mpc offers the following features:
nonlinear and economic model predictive control
support for differential algebraic equations (DAE)
time discretization with orthogonal collocation on finite elements
robust multi-stage model predictive control
moving horizon state and parameter estimation
modular design that can be easily extended
The do-mpc software is Python based and works therefore on any OS with a Python 3.x distribution. do-mpc has been developed by Sergio Lucia and Alexandru Tatulea at the DYN chair of the TU Dortmund lead by Sebastian Engell. The development is continued at the Laboratory of Process Automation Systems (PAS) of the TU Dortmund by Felix Fiedler and Sergio Lucia.
Example: Robust Multi-stage MPC#
We showcase an example, where the control task is to regulate the rotating triple-mass-spring system as shown below:

Once excited, the uncontrolled system takes a long time to come to a rest. To influence the system, two stepper motors are connected to the outermost discs via springs. The designed controller will result in something like this:

Assume, we have modeled the system from first principles and identified the parameters in an experiment. We are especially unsure about the exact value of the inertia of the masses. With Multi-stage MPC, we can define different scenarios e.g. \(\pm 10\%\) for each mass and predict as well as optimize multiple state and input trajectories. This family of trajectories will always obey to set constraints for states and inputs and can be visualized as shown below:
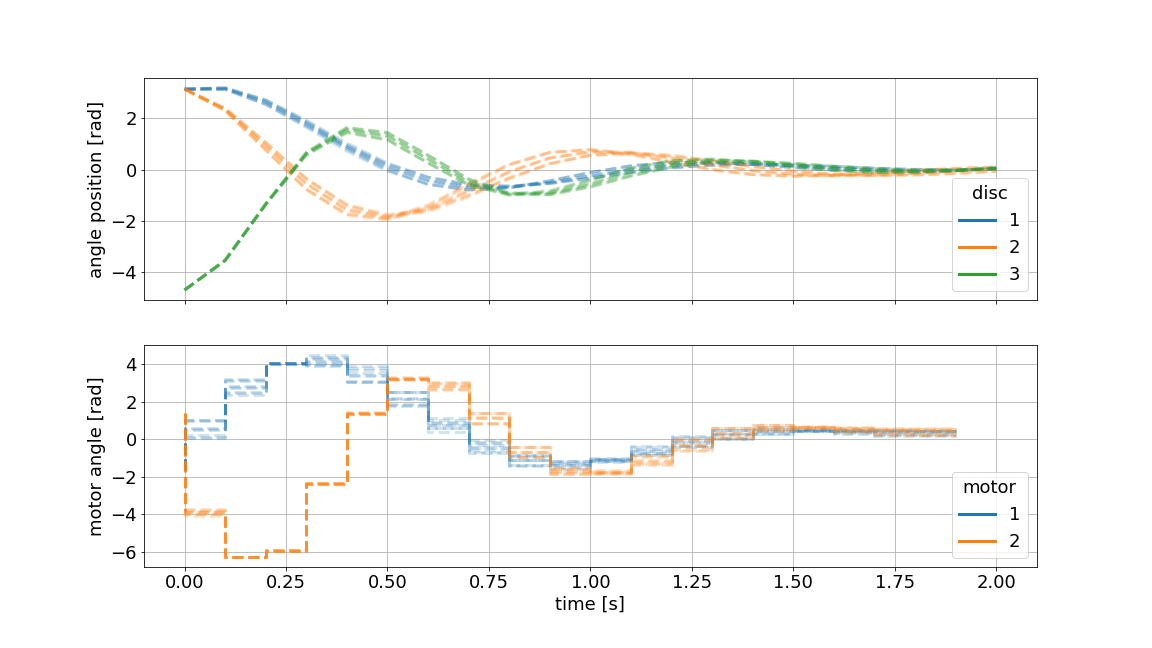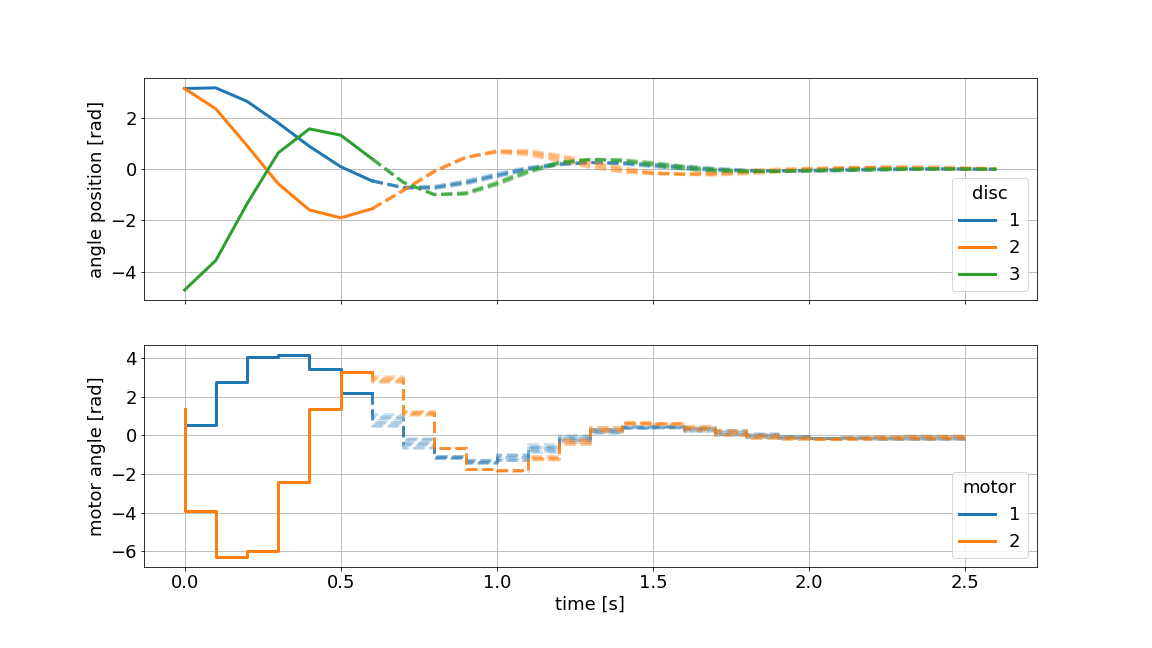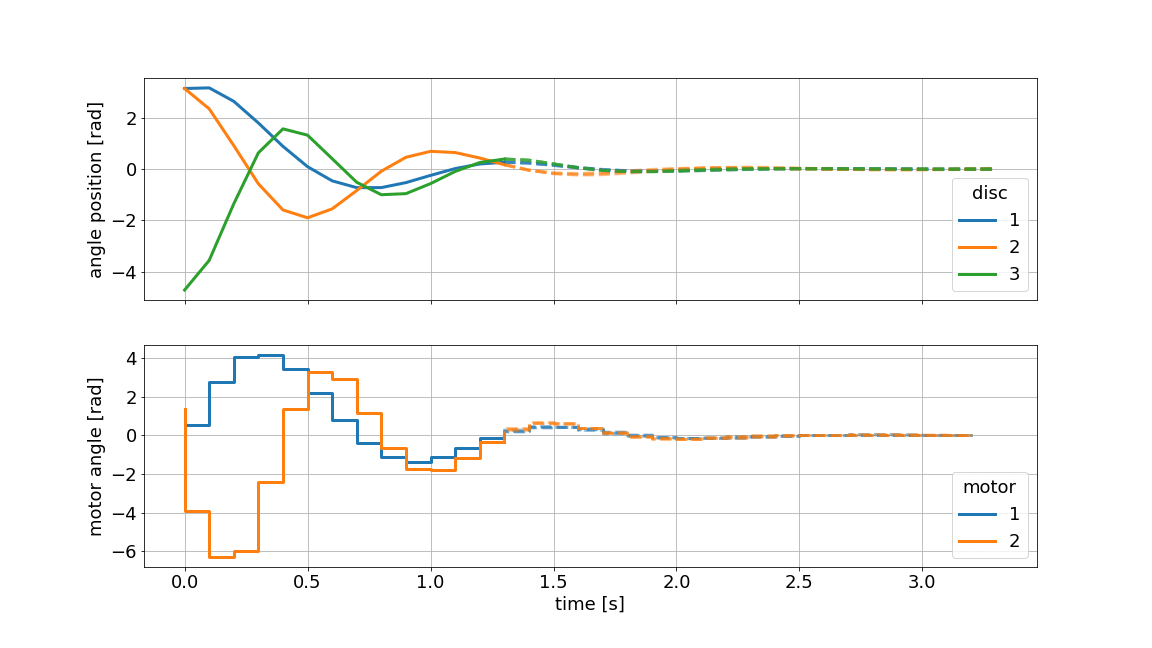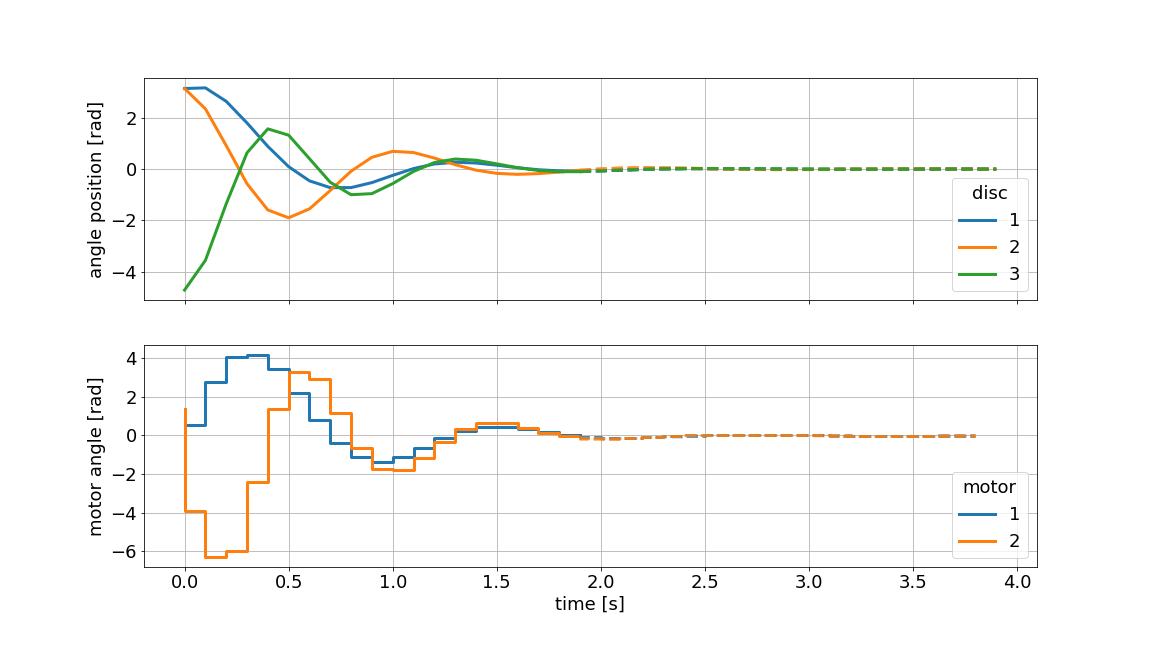
Example: Nonlinear MPC#
In the next example we showcase the capabilities of do-mpc to handle complex nonlinear systems. The task is to erect the classical double inverted pendulum (DIP) and navigate it around an obstacle.
The governing system equation is given as an implicit ODE:
which can be rewritten as:
and thus constitutes a a differential algebraic equation (DAE) which is fully supported by do-mpc.
The controller in this example is configured with an economic objective, where the task is to maximize the potential energy of the system while minimizing the kinetic energy.
An animation of the obtained controller results is shown below:
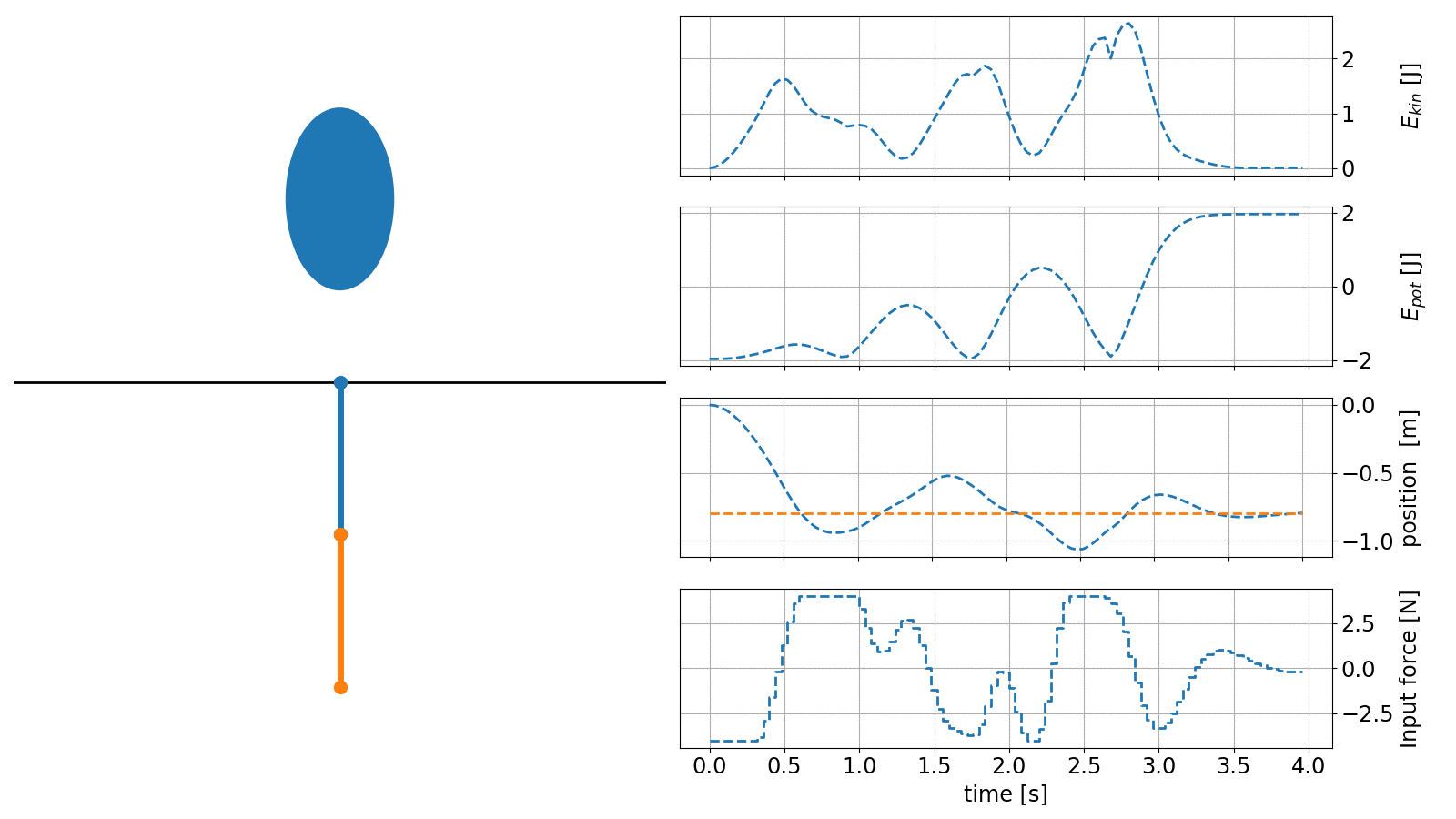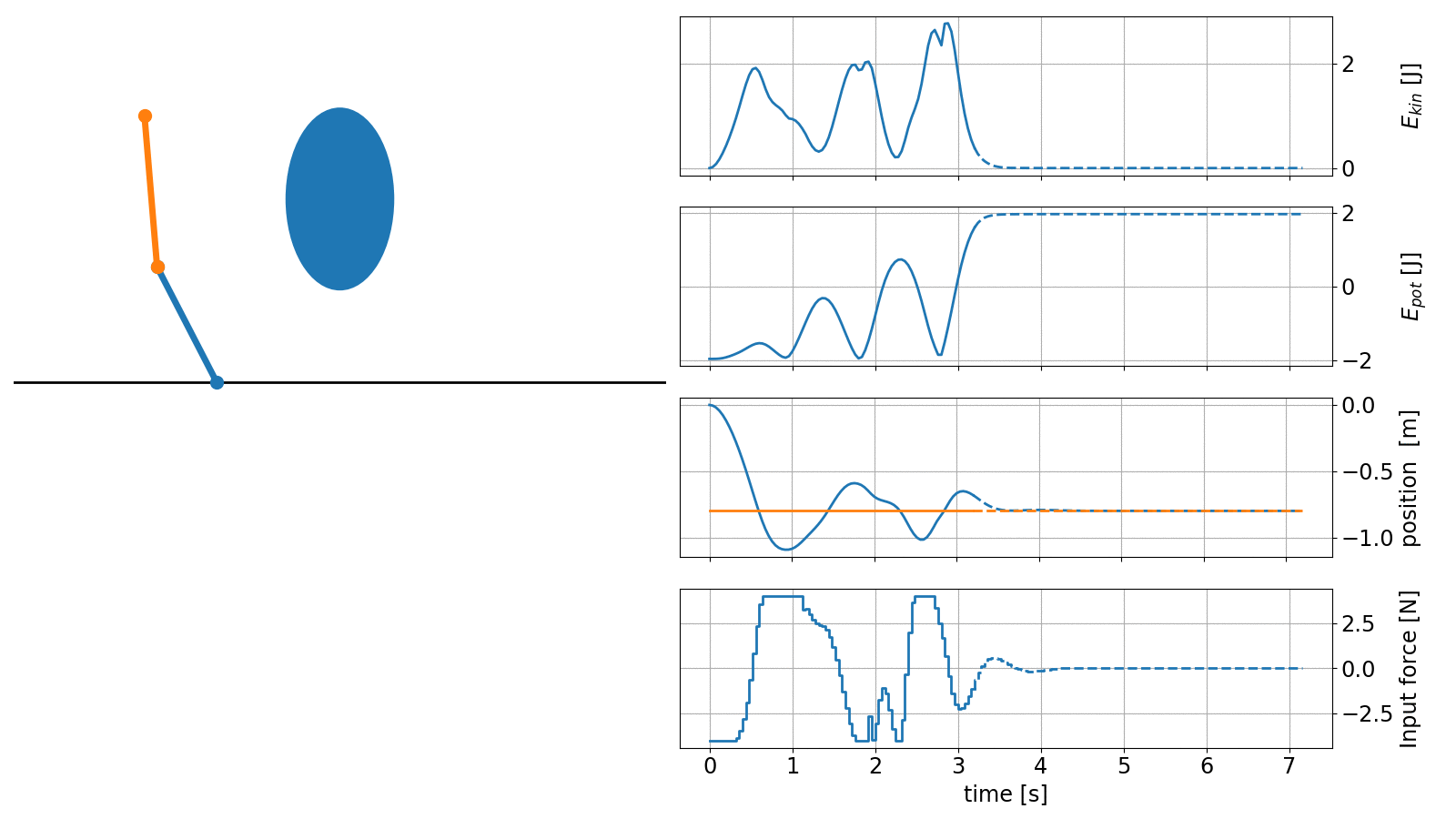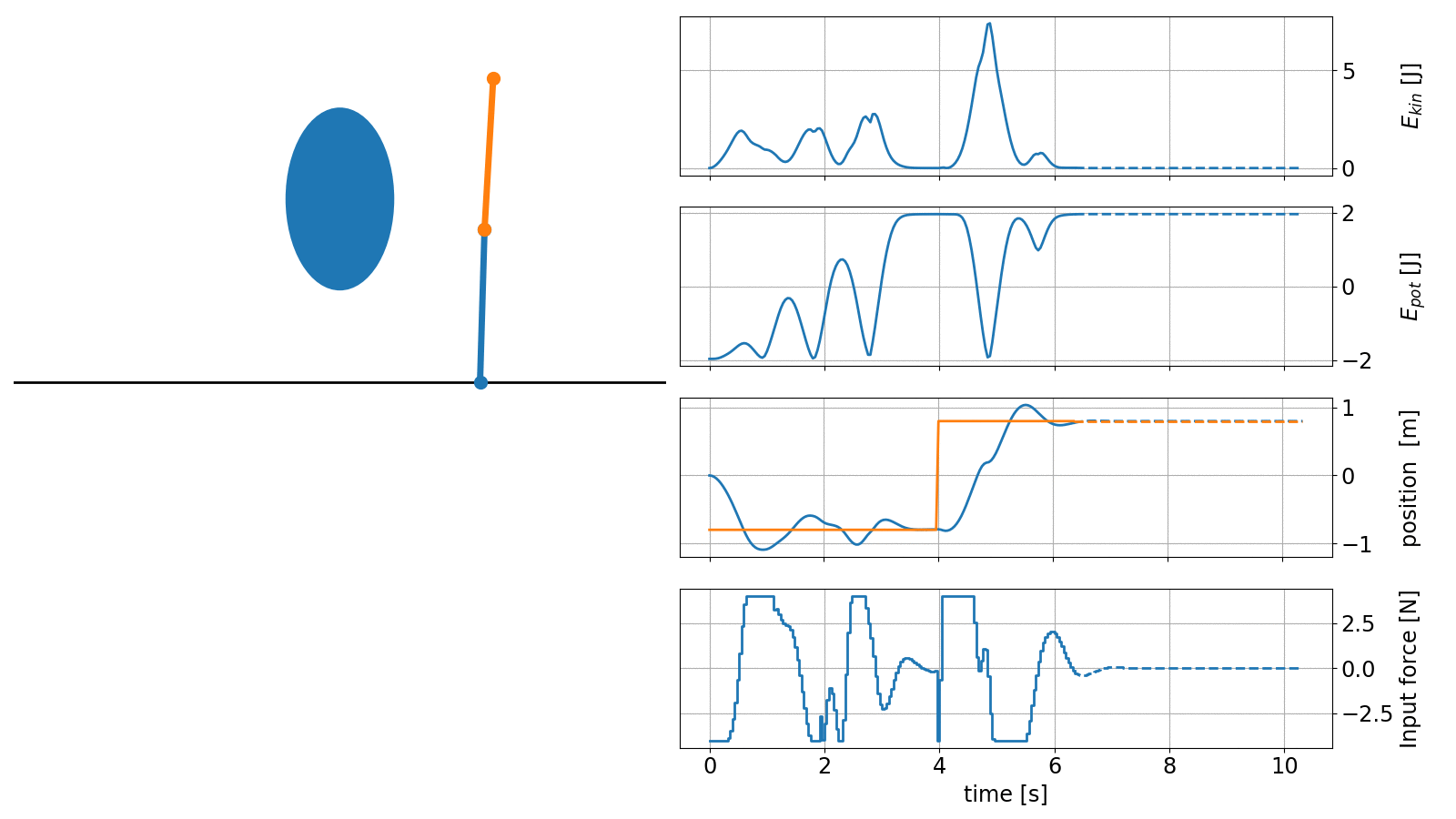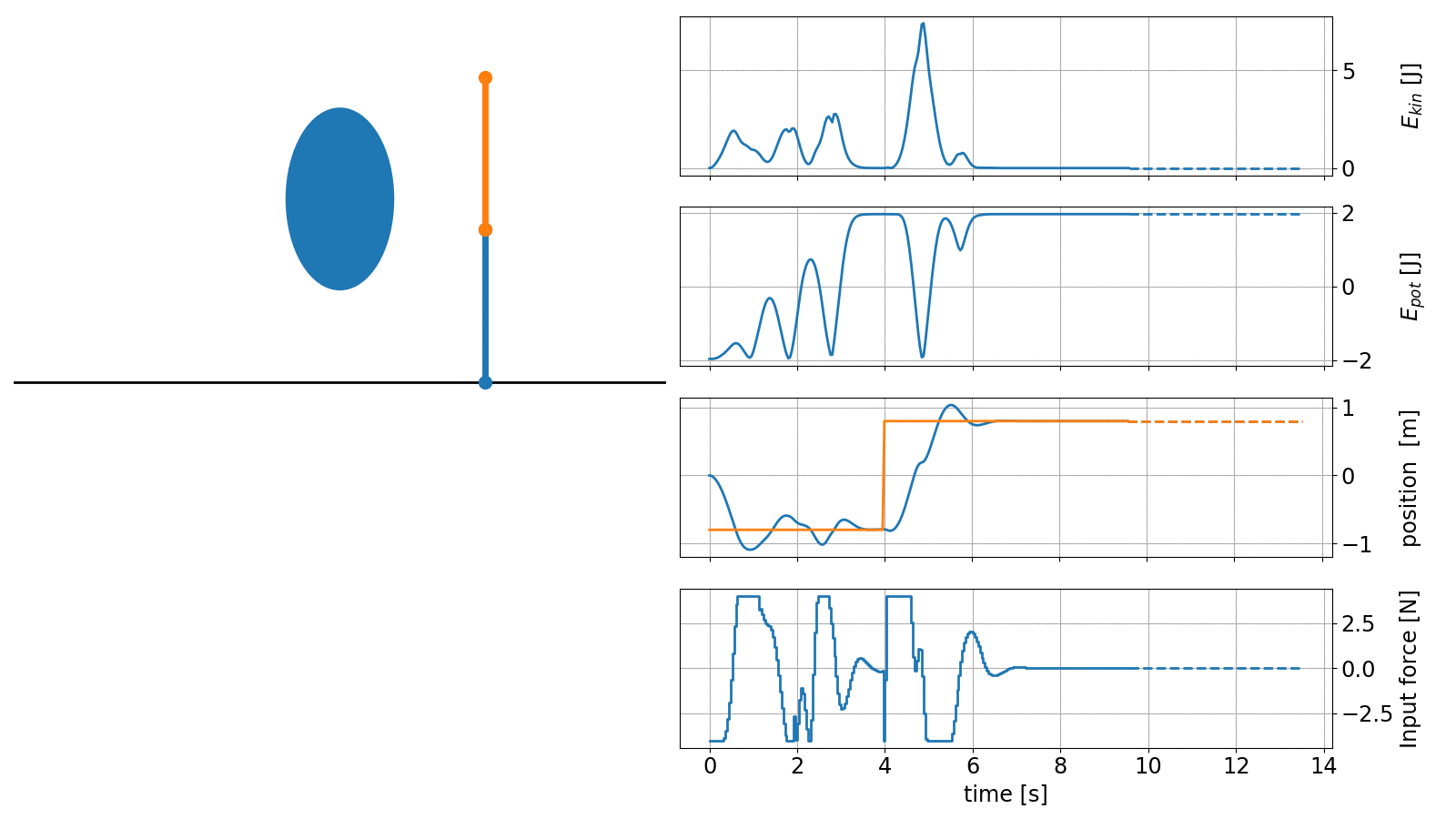
The code to recreate these results can be found in our example gallery.
Next steps#
We suggest you start by skimming over the selected examples below to get an first impression of the above mentioned features. A great further read for interested viewers is the getting started: MPC page, where we show how to setup do-mpc for the robust control task of a triple-mass-spring system. A state and parameter moving horizon estimator is configured and used for the same system in getting started: MHE.
To install do-mpc please see our installation instructions.
Table of contents#
Introduction
Background
How to get it?